Title: Are Emergent Abilities of Large Language Models a Mirage?

Institution: Computer Science, Stanford University

Authors: Rylan Schaeffer, Brando Miranda, Sanmi Koyejo

Arxiv Link: https://arxiv.org/abs/2304.15004

Comments: NeurIPS 2023

Date: 2023.04.28

前言

本文于2023.04.28在Arxiv上发布。前后两版，在NeurIPS 2023会议上获得了主会场最佳论文奖（2/3584）。

涌现现象 (Emergent ability)

图 1

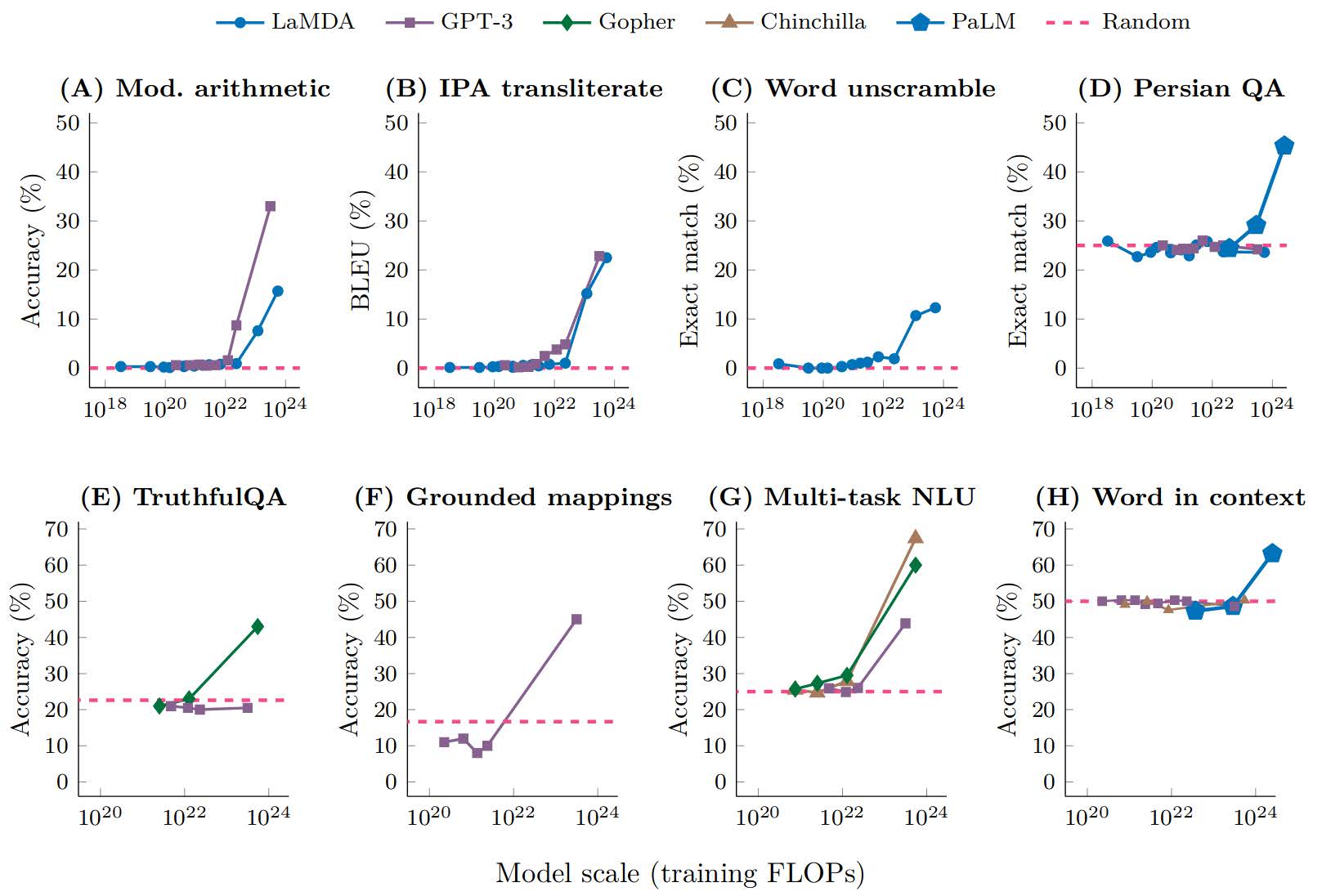
文章称有许多工作生成大型语言模型显示出涌现的能力，而这些能力在较小规模的模型中不存在，但在较大规模的模型中却存在，这就是人们常说的Emergent ability即涌现。

“emergent ability”（涌现能力）指的是当模型变得足够大时，它能展现出之前小模型所没有的新能力或行为，如某些性能指标陡然上升。

如上图所示，以LaMDA、GPT-3等系列模型为例，随着模型参数量的增加，当参数量达到某一临界点时，Accuracy陡然增加，这就是涌现。

Emergent ability有两个特点：

• Sharpness：随着参数量的线性增加，陡然上升
• Unpredictability：在某个不确定的临界参数量突然出现

涌现是否真的存在？

先说结论，本文揭示了大模型并不存在「涌现」，大模型的能力随着参数的增长是线性增长的。

产生涌现的真相是：涌现的出现并不是因为模型参数量的上升，而是因为研究者选择的度量指标导致的假象。

作者的出发点在于，前人度量模型能力的指标是离散的，而非线性的，会出现Emergent ability。然而，如果使用线性的或者连续的度量方式，模型的能力会不会是平滑、连续、可预测的呢？

Emergent Abilities的解释

图 2

作者首先自问自答，如何让模型性能中平滑、连续、可预测的变化显得陡然变化且不可预测？答案是，研究人员对非线性或不连续度量方式的选择可能会扭曲模型的性能表现，使其看起来陡然变化而不可预测。

过去的经验表明，神经网络的能力与训练数据及大小、参数量、耗费的计算资源成一定比例。根据这个经验，我们首先假设下式是正确的 (图 2.A) ： $$ \mathcal{L}_{CE}(N)=\left(\frac Nc\right)^\alpha $$ 其中，$L_CE$表示交叉熵，$N$表示参数量，$c>0$和$\alpha<0$为常数。 在实际应用中，交叉熵的定义为： $$ \mathcal{L}_{CE}(N)\overset{\mathrm{def}}{\operatorname*{=}}-\sum_{v\in V}p(v)\log\hat{p}_N(v) $$ 此公式衡量的是模型对整个词汇表 $V$的预测分布 $\hat{p}_N$真实分布 $p$之间的差异。对于每个可能的token $v$，真实分布$p(v)$表示token $v$出现的真实概率，而$\hat{p}_N(v)$是模型预测token $v$出现的概率。

由于 $p(v) = 0$对于所有 $v \neq v^*$，和 $p(v^*) = 1$，只有 $v = v^*$的项在求和中保留，公式简化为：

$$ \mathcal{L}_{CE}(N)=-\log\hat{p}_N(v^*) $$

每个token被正确预测的概率为 (图 2.B) : $$ \begin{align*} p(\text{single token correct})& =\exp\left(-\mathcal{L}_{CE}(N)\right)\\ & =\exp\left(-(N/c)^\alpha\right) \end{align*} $$ 假设研究人员随后选择了需要正确选择$L$个token的度量方法。例如，任务可能是$L$位数整数加法，如果模型的所有$L$个输出数字完全与所有目标数字匹配，没有增加、删除或替换，就得分为$1$，否则得分为$0$。如果每个标记正确的概率是独立的，那么得分为$1$的概率为： $$ \begin{align*} \operatorname{Accuracy}(N) &\approx p_N\left(\text{single token correct}\right)^\text{num. of tokens} \\ &= \exp\left(-(N/c)^\alpha\right)^L \end{align*} $$

$$\text{Exact String Match}\stackrel{\text{def}}{=}\begin{cases}1&\text{if output string exactly matches target string}\\0&\text{otherwise}\end{cases}$$

这种度量方法的选择会使得性能随着标记序列长度的增加而非线性缩放。当在linear-log图上绘制性能时 (图 2.C)，可以看到更长序列上出现了陡然上升、不可预测的突变，这与其他学者所声称的涌现能力非常吻合。

而如果使用线性的度量方式Token Edit Distance又会出现什么呢？ $$ \begin{aligned} \text{Token Edit Distance}(N) &\approx L(1-p_N(\text{single token correct})) \\ &= L\left(1-\exp\left(-(N/c)^\alpha\right)\right) \end{aligned} $$ 当使用线性的度量指标Token Edit Distance来衡量模型的能力时，模型的能力变得平滑、连续、可预测 (图 2.E)。

“标记编辑距离”（Token Edit Distance）是一种度量两个序列差异的方法。它计算的是将一个序列转换成另一个序列所需的最小编辑操作数，这些操作包括插入、删除和替换单个标记。在这里的上下文中，一个"标记"（token）通常指的是一个词、字符或者其他的语言单位。

举例来说，如果我们有两个词序列，序列A是“cat”而序列B是“bat”，那么序列A变为序列B的标记编辑距离是1，因为只需将“c”替换为“b”即可。

如果使用离散的度量指标Multiple Choice Grade，则会观察到涌现现象 (图 2.D)，但是如果使用连续度量指标Brier Score，涌现现象则会消失 (图 2.F)。

Multiple Choice Grade：

$$\\ \text{Multiple Choice Grade}\stackrel{\text{def}}{=}\begin{cases}1&\text{if highest probability mass on correct option}\\0&\text{otherwise}\end{cases}$$

Brier Score： $$ BS = \frac{1}{N} \sum_{i=1}^{N} (f_i - o_i)^2$$ 其中：

• $N$ 是预测的数量。
• $f_i$是第$i$个预测的发生概率（模型预测的概率）。
• $o_i$是第$i$个实际发生结果的观察值（通常用1表示事件发生，用0表示未发生）。

举例来讲，假设你正在预测一个足球比赛是否会打平。对于三场比赛，你的模型预测打平的概率分别为0.3、0.6和0.2。实际结果是第一场比赛打平了（1），而第二场和第三场没有（0）。

那么，Brier Score将计算如下：

• 对于第一场比赛，预测误差为 $ (0.3 - 1)^2 = 0.49 $。
• 对于第二场比赛，预测误差为 $ (0.6 - 0)^2 = 0.36 $。
• 对于第三场比赛，预测误差为 $ (0.2 - 0)^2 = 0.04 $。 Brier Score是这些误差的平均值，所以在这个例子中，Brier Score为 $ \frac{0.49 + 0.36 + 0.04}{3} = 0.2967 $。

总结来讲，造成涌现现象的假象有两点

1. 前人采取的度量标准是离散的而非连续的或线性的，从而导致出现涌现现象的出现。
2. 前人只在模型参数量的小范围内进行实验。具体而言，一般模型的大小有6b，7b，13b，33b，70b等，这些模型参数量只覆盖了很小的一部分范围。如果有6b，6.1b，6.2b，6.3b…70.1b，70.2b等大小人们就会观察到离散的度量标准与模型参数量间呈指数关系，而不是突变关系。

本文作为NeurIPS 2023的Best paper可谓实至名归，虽然研究基于简单的出发点，但论文提出了有深远影响的见解，极富创造性和启示价值。在本文发表之前，涌现现象一度成为业内公认的“神奇现象”，关于此现象的研究开展了很多包括使用探针进行实验等，但本文在此情况下从细节入手，揭示“涌现”其实不存在令包括笔者在内的许多研究者醍醐灌顶。