Title: Fewer is More: Boosting LLM Reasoning with Reinforced Context Pruning

Institute: Hong Kong University of Science and Technology, Microsoft Research

Authors: Xijie Huang Li, Lyna Zhang, Kwang-Ting Cheng, Fan Yang, Mao Yang

Arxiv Link: https://arxiv.org/abs/2312.08901

Date: 2024.2.15

一、摘要

即使使用了CoT，LLMs在解决数学推理问题的表现依旧不尽人意。作者提出CoT-Influx方法，一种对CoT的示例和内容进行优化从而提高LLMs推理能力的方法，其核心思想是通过剪枝最大化有效信息的输入。

二、动机

1. 链式推理示例（Chain-of-Thought, CoT）的潜力未被充分利用：
   之前的研究表明，提供分步的链式推理示例可以帮助模型更好地进行复杂推理。然而，由于模型的上下文窗口长度（context window size）有限，能够输入的CoT示例数量受到限制，因此无法完全发挥CoT的潜力。

2. 现有解决方案的局限性：
   扩展上下文窗口虽然可以容纳更多的CoT示例，但会增加推理成本和复杂度，代价高昂。而现有的基于压缩或检索的技术在数学推理任务上表现不佳，尤其是无法有效地选择对特定任务最有帮助的CoT示例和token。

基于这些动机，本文提出了CoT-Influx方法，旨在解决上述问题。其目标是通过剪枝策略，在不增加计算成本的前提下，增加输入文本的质量。

三、观察

1. 更多的CoT示例可以提升LLMs推理性能： 增加CoT示例的数量能够提升LLMs在数学推理任务中的表现，但受限于上下文窗口长度，LLMs无法输入足够多的示例。

2. CoT示例选择至关重要： 并非所有的CoT示例都有助于推理，随意添加错误、冗余、误导的示例甚至可能导致性能下降。

3. CoT示例中存在冗余token： CoT示例中往往包含不必要的冗余token，这些token可以被剪枝以腾出更多空间容纳更有用的内容，从而提高推理效果。

四、方法：CoT-Influx

简要不看细节版

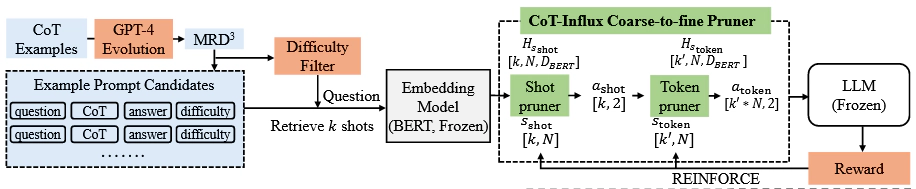
CoT-Influx将LLM视为黑盒，关键模块是一个粗糙到精细的剪枝器，目的在于生成高质量、低长度的CoT示例，包括两个步骤：

1. 样本剪枝（Shot Pruner）：首先，从一大批CoT示例中筛选出对目标问题最有帮助的k个示例。

2. 标记剪枝（Token Pruner）：接着，从这些被保留下来的CoT示例中进一步剪枝，移除不重要的token，生成精简版本。

最后，将精简后的CoT示例拼接在问题前面，完成！

细节版

1. 问题定义

给定一个链式推理示例集合 $\mathcal{D} = \{x_{\text{cot}}^i\}_{i=1}^{n}$，每个示例 $x_{\text{cot}}^i$ 由问题、推理步骤和答案组成，且其token数量超出LLM的上下文窗口长度 $T$。我们希望通过两阶段的剪枝过程，对 $\mathcal{D}$ 进行优化，生成有效输入，使其token总数 $t(x_{\text{input}})$ 满足：

$$ t(x_{\text{input}}) \leq T $$

同时保证LLM能够基于此输入生成正确的推理结果。

2. 两阶段剪枝过程

CoT-Influx的两阶段剪枝过程通过策略网络选择有用的链式推理示例和相关token，具体描述如下：

• 第一阶段：样本剪枝（Shot Pruner）
  该阶段使用一个包含两层隐藏层的多层感知机（MLP）从一批链式推理示例中选择出最有用的 $k'$个示例。MLP的输入是每个示例的文本嵌入向量，表示为 $H_{\text{shot}} \in \mathbb{R}^{k \times N \times D_{\text{BERT}}}$，其中 $k$是批量大小， $N=512$是每个示例的token数， $D_{\text{BERT}}$是BERT嵌入的维度。MLP经过计算后输出一个概率分布：

$$ \pi_{\theta_1}(a_{\text{shot}} | s_{\text{shot}}) = \sigma(\text{MLP}(H_{\text{shot}})) $$

其中， $\sigma$为Sigmoid激活函数，动作 $a_{\text{shot}}$表示是否保留该CoT示例。选择后的示例集为：

$$ \mathcal{D'} = \{x_{\text{cot}}^j \in \mathcal{D} : a_{\text{shot}}^j = 1\} $$

• 第二阶段：token剪枝（Token Pruner）
  对保留下来的示例集 $\mathcal{D'}$，使用另一层包含两层隐藏层的MLP进一步剪枝每个示例中的token。类似地，MLP的输入是保留示例的嵌入向量 $H_{\text{token}} \in \mathbb{R}^{k' \times N \times D_{\text{BERT}}}$，输出概率分布决定每个token是否保留：

$$ \pi_{\theta_2}(a_{\text{token}} | s_{\text{token}}) = \sigma(\text{MLP}(H_{\text{token}})) $$

剪枝后的token集为：

$$ \hat{x}_{\text{cot}}^j = \{ \text{token} \in x_{\text{cot}}^j : a_{\text{token}} = 1 \} $$

3. 优化目标：多目标奖励函数

CoT-Influx的优化目标就是通过一个多目标奖励函数，在保持推理准确性的同时，尽量减少冗余的示例和token。这个奖励函数综合了LLM的推理损失、推理的准确性和输入的token数量。具体定义为：

$$ R(x_{\text{input}}) = \left( \frac{1}{1 + L_{\text{LLM}}(x_{\text{input}})} + R_{\text{Acc}} \right) \times \left( \frac{t(x_{\text{input}})}{T} \right)^w $$

其中：

• $L_{\text{LLM}}(x_{\text{input}})$ 表示LLM的推理损失；
• $R_{\text{Acc}}$ 是推理的准确性（正确时为1，错误时为0）；
• $t(x_{\text{input}})$ 是输入的token数量；
• $T$ 是上下文窗口的最大token长度；
• $w$ 是用于调整token数量影响的超参数。

通过这个多目标奖励函数，CoT-Influx引导剪枝器最大化推理准确性，并尽量压缩输入token的总量，确保输入不超出上下文窗口长度。

4. 强化学习优化

为了优化剪枝策略网络，CoT-Influx使用了REINFORCE进行优化，通过最大化奖励函数来调整两阶段剪枝器的参数。

$$ \nabla_\theta J(\theta) = R(x_{\text{input}}) \cdot \left( \nabla_\theta \log \pi_{\theta_1}(a_{\text{shot}} | s_{\text{shot}}) + \nabla_\theta \log \pi_{\theta_2}(a_{\text{token}} | s_{\text{token}}) \right) $$

五、结果

下图展示了CoT-Influx在GSM8K数据集上的表现

值得注意的是，如下图所示，LLaMA2-70B搭配CoT-Influx在没有任何微调的情况下超过了更大的LLMs。比如LLaMA2-70B相比GPT-3.5提高了2.5%。

六、发现

1. 更具能力的LLM偏爱更难的CoT示例，而较小的LLM则选择更简单的示例。
2. 数字和格式标记对于数学推理至关重要。像with、the、then这样的功能词，以及与推理能力无关的背景环境，如theater,可以被剪掉而不影响推理能力。

七、评价

1. 虽然思路很自然，这篇文章还是具有一定的启发性的，尤其是对架构的设计和优化部分。

2. 这篇文章讲故事的水平是很高超的，可以把来龙去脉讲的非常吸引人，比如Pilot Study部分。能把简单的东西讲的很高深但却易于理解。

3. 在实验上有很多可以学习的地方，比如消融实验和许多小的实验，逻辑很严谨。

4. 在实用性上有待讨论，首先使用强化学习的方法就意味着这种方法对成本是有一定需求的。其次，我认为这个方法是一个端到端的设计，如果换数据集就需要重新训练。最后，也许这个网络训练出来删除掉的就是with、the、then这样的词，如果真是如此死板，那不如使用词表的方法。当然此条只是推测。