前言

由于笔者最近开展LLM enhance Graph相关的工作，因此对图上的启发式算法产生了一定的兴趣。通过搜索引擎发现了这篇发表于2006年的综述性论文。尽管文章的发表时间比较久远，但是一来最短路算法在近20年并不是热门研究领域因此新工作很少，二来最近很多LLM Reasoning方向的论文的灵感都来源于传统算法，因此在此对该文章进行提炼和总结。

介绍

尽管标准的最短路最优算法已经可以解决大部分的最短路问题，但是在大规模图、低时延的任务中标准最短路算法往往不能满足任务的需求。例如，在车载路线导航系统，需要立即响应。而在这些任务中，一些任务对结果的要求不一定是“最优的”，而是“较优的”，因此启发式最短路算法应运而生。

在过去的六十年间，有学者提出了许多启发式方法来减少最短路径算法的计算时间。本文对过去开发的各种启发式最短路径算法进行了调查和回顾。

最短路问题及最优算法

设有向图为$G(N,A)$构成，图中有$N$个顶点，$A$条有向边。$n = |N|$表示顶点的个数，$m = |A|$表示边的个数。$a=(i,j)\in A$表示一条从$i$到$j$的有向边，$c_{i,j}$ 表示从$i$到$j$的代价。一条从起点$o$到终点$d$的路径可被定义为$path = (o,j),\ldots,(i,d)$，其代价为每一条边的代价的总和$cost_{path} = \sum_{(i,j)\in path} c_{i,j}$。最短路径问题就是找到使$cost$最小的路径 $path = {\arg \min}_{path \in \text{all paths}} (cost_{path})$。

最优算法

这个最短路径问题(SPP)已经在不同的领域研究了 40 多年，如计算机科学和交通。由于它们的计算可操作性，这一领域的大多数研究都集中在开发日益高效的最优算法来解决该问题。大多数最优最短路径算法本质上是动态规划理论在图中搜索最短路径方面的应用。最短路径是通过从源节点到目的节点的递归决策过程来找到的。

大多数最短路径算法都遵循下面这样一个标准程序：

1. 初始化：

   $\begin{array}{l}i=o;L_{(i)}=0;L_{(j)}=\infty;\forall j\neq i;P_{(i)}=\text{NULL.}\\Q=\{i\};\end{array}$

2. 节点选择：

   选择并从$Q$中删除节点$i$

3. 扩充节点

   扫描从$i$出发的边. 对于边 $\alpha=(i,j)$ 如果 $L_{(i)}+c_{a}<L_{(j)}$ 则 $L_{(j)}=L_{(i)}+c_{a};P_{(j)}=a$ 将$j$插入集合$Q$

4. 停止检查

   如何$Q = \emptyset $则停止，反之，重复Step 2

其中，从原节点$o$到节点$i$的代价被定义为$L(i)$，$P$表示存储到每个节点的最短路径树上来自的边的列表，$P(i)$表示到节点$i$的最短路径上的来自的边，$Q$表示待扫描的节点集，它管理着搜索过程中要检查的节点。

Label-setting algorithm (LS)

$Q$中的元素根据当前的代价进行排序

它的一个显著特点是，如果只需要从起始节点到单个目的地节点的路径，当目的地节点的代价被计算出来时，算法就可以终止。这种类型的操作通常被称为一对一搜索模式。

如dijkstra。

Label-correcting algorithm (LC)

$Q$中的元素在最短路径树构建的过程中被填充和扫描。

它的特点是，在确定到网络中每个节点的最短路径之前，它不能提供两个节点之间的最短路径，称为一对多搜索模式。

如Bellman-Ford、SPFA。

计算性能

在 LC 算法中，双端队列（double ended queue）和阈值列表结构（threshold list data structures）在计算效率方面占主导地位。

在 LS 算法中，Dial的桶实现（Dial’s bucket implementation）和二进制堆结构（binary heap data structure）是最有效的。

启发式最短路算法

在上文中讨论的最优最短路径算法，对于现实中的实时问题来说，计算量往往太大。

这种“低效”源于这样一个事实：这些算法采用了“无信息量”的向外搜索技术，没有利用关于起点和 终点节点的位置、路径组成和网络结构的先验知识。

例如，如果起始节点位于城市中心，而目的节点位于城南，那么优化算法搜索原点节点以北的最小路径路线的可能性与搜索原点节点以南的可能性相同。

直观地说，如果在搜索过程中使用更多的信息，算法的效率就可以提高。后一点很早就被 AI 领域的研究人员认识到，并提出了许多启发式方法，试图使用各种额外知识来源来减少搜索工作。

启发式搜索策略一般可以分为四种策略：

1. 限制搜索区域（Limit the search area）
2. 分解搜索问题（decompose the search problem）
3. 限制搜索的边（limit the links searched）
4. 上述的某种组合

接下来，我们将研究这些启发式搜索策略及其在最短路径搜索中的应用。

限制搜索区域

“限制搜索区域”策略背后的思想是利用一些关于从原点节点到目的节点的最短路径的先验知识，将最短路径搜索限制在一定的区域内。

由此产生的搜索区域将比无先验知识的最优算法的搜索区域小得多。

剪枝

此基本思想试图通过“修剪”那些几乎不可能到达目标节点的最短路径上的中间节点来限制搜索区域。

在经典的城市交通网络中，每个路段(或路段)通常只与相邻节点(如路口)相连，路段上的旅行时间通常与其长度相关。这个性质使搜索区域被限制在原点节点和终点节点周围的指定区域内。这个区域之外的节点被假定在最短路径上的概率很小，因此在搜索过程中无需进一步检查就可以被排除。

问题的关键在于定义搜索区域，这样可以有效地减少计算时间，同时获得一个好的解决方案。

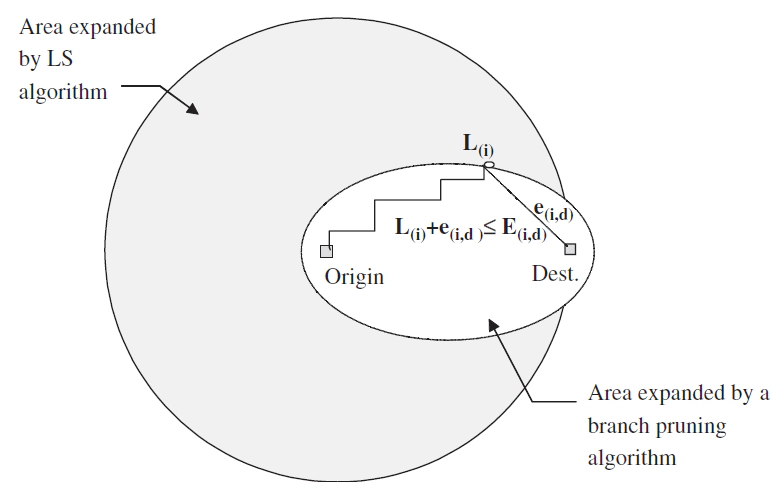
有学者提出使用下式约束搜索范围： $$ L_{(i)}+e_{(i,d)}\leqslant E_{(o,d)}, $$ 其中，$L(i)$是当前从原点节点 $o$ 到节点 $i$的最小代价；$e(i,d)$表示节点$i$到目的节点$d$的预计代价；$E(o,d)$表示从起点节点到目的节点的最小代价的上界。

将该方法加入到LC最优算法的过程中只需要对Step 2进行修改

2. 选择并从$Q$中删除节点$i$。如果$L_{(i)}+e_{(i,d)}\leqslant E_{(o,d)}$则跳到第四步。

分支修剪算法的效率如上图所示。可以看出新的启发式策略将搜索区域从最优 LS 算法展开的圆缩小到椭圆。在理想的欧几里得网格中，这些启发式算法的搜索区域可能小到LS 算法的搜索区域的20%。

分支剪枝最短路径算法的效率和精度取决于估计函数$e(i,d)$和 $E(o ,d )$的质量。易见，只有当估计$e(i,d )$始终低于从节点$ i $到目的节点$ d $的最小代价，同时$E(o ,d)$的估测值大于从原点节点$ o $到目的节点$ d $的最小代价时，剪枝算法的最优性才会保留。此外，可以注意到，当$e(i,d )$趋近于零、 $E(o,d )$趋近于无穷时，分支剪枝算法将成为最优最短路径算法。

简而言之，使用上述方法时，$e$要往小估，$E$要往大估。

A*

在剪枝方法中，具有低概率在最短路径上的节点被修剪。而A*算法将这些节点保持在$Q$中，但给它们分配低优先级。

A*算法利用了一个启发式的评估函数$F_{(i)}=L_{(i)}+e_{(i,d)}$作为节点$i $的标签，其中$ L(i)$是当前评估路径从原点节点到节点$ i $的代价，$e(i,d)$是从节点$ i $到目的节点$ d $的估计代价。两个函数的和$F$反映了$i$在最短路上的可能性。$F$越高，$i$越可能出现在最短路上。基于这个思路，该算法执行了一种最优先搜索，即它维护一个按照它们的$F$值排序的节点列表$Q$以供扫描，并选择一个$F$值最低的节点进行扩展。被选中的节点通过访问它的邻接点来扩展，根据邻接点的$F$值，将邻接点有序放入$Q$中。这一过程持续进行，直到选择目的节点进行扩展。因此，A*算法与LS算法有相似之处。

此处推荐一个了解A*算法的文章，逻辑清晰且提供了交互页面：https://www.redblobgames.com/pathfinding/a-star/introduction.html

与LS算法相比，A*使用评估函数是$F(i)$来确定$Q$中的节点顺序而不是$ L ( i)$。

主要的区别在于Step 3，修改如下:

3. 扩充节点

   扫描从$i$出发的边。对于边 $\alpha=(i,j)$ 如果

   $L_{(i)}+c_{ij}+e_{(j,d)}<F_{(j)},$

   则

   $\begin{array}{l}L_{(j)}=L_{(i)}+c_{ij};F_{(j)}=L_{(i)}+c_{ij}+e_{(i,d)};P_{(j)}=a,\end{array}$

   将$j$插入集合$Q$

由于A*算法基于最优优先思想，因此满足以下不等式的节点将在算法终止之前被扫描 $$ L_{(i)}+e_{(i,d)}\leqslant L_{(d)}. $$ 因此，只要估计函数不要高估代价，就可以找到最优解。

分解搜索问题

人们普遍认识到，解决一个通用搜索问题所需的计算量通常比问题本身的规模增长得更快。例如，从一个起始节点到一个目标节点找到最短路径所需要的计算时间取决于在到达目标节点之前搜索的节点数，因此计算量是距离的高阶多项式函数。因此，如果原始问题可以分解为更小的子问题，就可以大量降低复杂度。

本节介绍了如何使用双向搜索方法和子目标方法来实现这种策略。

双向搜索策略

双向搜索策略试图将搜索过程划分为两个独立的过程。一个从起始点向前推进，另一个从结尾向回推进。当这两个搜索过程在某个中间阶段相遇时，就找到了解决方案。

如上图所示，该算法将同时从起点和终点向外构建最短路径树，直到满足某种停止条件为止。

双向算法的效果受两个因素影响。

1. 前向和后向的算法的交替规则
2. 算法什么时候停止

对于前者，最直观的方法是平等交替。然而，平等交替不一定是最高效的。最好的策略应该在扫描最少的节点下找到最短路径。

对于后者，有学者提出下式： $$ L_{(i)}^o+L_{(i)}^d\leqslant\min_{j\in N}{L_{(j)}^o}+\min_{j\in N}{L_{(j)}^d} $$ 这个式子的意思反应的是，对于任意节点$j$，从$o$到$j$的最小代价加上从$j$到$d$的最小代价大于等于$o$到$d$经过$i$的最短距离。此时，$i$一定是$o$到$d$的最短路上的一个节点。

然而聪明的读者很快就会发现，这是一个相当愚蠢的判断标准。

果不其然，有学者证明，当使用这个停止准则时，由此产生的双向搜索算法不如单向算法。据推测，由双向搜索过程扩展的节点可能在满足条件之前生长成几乎完全的单向树，而不是在起点和终点之间的“中间”相遇。

后又有多位学者在此基础上进行改进。如使用改变了估计函数的双向A*算法、使用多个相遇的中间节点的双向A*算法等。

子目标方法

子目标可以定义为问题最优解的中间状态。对于道路交通网络中的最短路径搜索问题，子目标可能是位于起点和终点之间的那些节点或边，需要确定它们之间的最短路径。如果预先知道子目标的位置，那么从起点到终点寻找最短路径的问题可以分解为两个或更多较小的问题。

例如，如果有一个子目标节点，原始问题可以通过解决两个子问题来解决：一个是找到从起点到子目标节点的最短路径，另一个是找到从子目标节点到终点的最短路径。

如果已知一个子目标节点，并且位于从起点到终点的最短路径的中间，那么使用这个子目标节点将使搜索区域与LS算法相比减少大约50%，如图上图所示。如果同时使用了限制搜索区域的技术之一，计算节省将会更大。

此方法可行的原因在于，如果我们已知$i$是从$o$到$d$的最短路上的一个中间节点，那么从$o$到$d$的最短路的代价一定等于从$o$到$i$的最短路的代价加上从$i$到$d$的最短路的代价。

限制搜索的边

在最短路径搜索过程中，每次迭代期间的主要决策涉及从每个节点发出的边的扫描。在传统的最短路径算法中，当选择一个节点进行扩展时，将扫描来自该节点的所有边， 无论它们在最短路径上的可能性有多大。

限制搜索的边的基本思想是跳过对那些要么在最短路径上，要么在实际情况中使用的概率很低的边的检查。通过使用下一节讨论的分层搜索方法，可以有效地实现这一思想。

分层搜索

分层搜索背后的基本思想是，为了有效地找到一个复杂问题的解，搜索过程首先应集中在问题的本质特征上，而不考虑较低层次的细节，然后再完成细节。

举例来讲，在驾驶者查找两个地点的路线的问题中，我们先找到需要路径中的主干道，然后再找这些主干道间的小路。通过“先找到需要路径中的主干道”就可以将搜索的范围缩小至所有主干道，而“再找这些主干道间的小路”则将搜索范围缩小至与这些主干道相连的小道。

此方法有两个问题需要解决

1. 如何将现实道路映射到分层图中？
2. 如何控制不同层间的转换？什么时候切换到下一个层？

高速公路和交通大动脉是为长距离运输而设计的，而地方的街道则主要用于当地车辆出行。因此，道路连接可以根据它们的功能方便地分类。有学者提出以边的长度为标准，提取长边形成高层子网络，并将较短的边及其节点分组为低层子网络。又有学者提出根据限速、车道数等属性将所有道路划分为高低两级。

分层搜索算法的一个问题在于无法在两个主干道间走捷径。比如通过使用住宅区道路从一条主干道转到另一条主干道。分层搜索算法在设计时是为了简化搜索过程，通过将道路分为不同的等级（如高速公路、干道、住宅道路等）来减少需要考虑的道路数量。这种方法通常会首先考虑等级较高的道路（如高速公路），而不是等级较低的道路（如住宅道路）。

Reference

Title: Heuristic shortest path algorithms for transportation applications: State of the art

Institute: University of Waterloo, Chongqing University, University of Nebraska-Lincoln

Authors: L. Fua, D. Sunb, L.R. Rilettc

DOI: https://doi.org/10.1016/j.cor.2005.03.027

Date: 2006.11.01